Wellengleichung

Falls numpy etc. auf Schulrechnern nicht verfügbar:

https://trinket.io/embed/python3/a5bd54189b

(alle Programme recht rasch erstellt, geht sicher eleganter…) Die Mathematik und Formeln für die Iteration sind hier noch nicht dokumentiert (bisher an Tafel erklärt). Wellengleichung $u_{tt}=\Delta u$ bzw. $v=u_t$ und $v_t=\Delta u$.

Lernen, wie man den Graphen einer Funktion zeichnet (function plot)

Bitte Programm ausklappen

import numpy as np
from matplotlib import pyplot as plt
from matplotlib import colormaps
import matplotlib.animation as animation
from matplotlib.animation import FuncAnimation
 
# maximale x-Koordinate.
n = 40
 
# Gezeichnet werden soll die folgende Funktion f.
# Bitte damit herumspielen.
def f(x):
    return 100 * np.sin(x * 3 * np.pi / n)
 
# Die Liste u wird die Funktionswerte von f an allen ganzzahligen Argumenten zwischen 0 und n-1 enthalten.
# Zuerst wird sie initialisiert (alle Einträge Null).
u = np.zeros(n)
# Dann werden die Funktionswerte von f berechnet.
for x in range(n):
    u[x] = f(x)
 
fig, ax = plt.subplots()
# Ausdehnung der y-Achse.
ax.set(xlim=(0, n), ylim=(-100, 100))
 
# Die Plot-Funktion benötigt zu jedem y-Wert den zugehörigen x-Wert.
# Der folgende Befehl erstellt eine Liste aller ganzan Zahlen von 0 bis n-1.
x_werte = np.linspace(0, n, n)
 
ax.plot(x_werte, u)[0]
plt.show()

Lernen, wie man den Graphen einer zeitabhängigen Funktion animiert zeichnet

Bitte Programm ausklappen

import numpy as np
from matplotlib import pyplot as plt
from matplotlib import colormaps
import matplotlib.animation as animation
from matplotlib.animation import FuncAnimation
 
# maximale x-Koordinate.
n = 40
iterationen = 1000
geschwindigkeit = 20 # je höher, desto schneller
 
# In der folgenden Funktion ist i die Iterationsvariable = die Zeit.
# Zur Zeit i soll die Funktion f(i, ?) gezeigt werden.
# Bitte damit herumspielen.
def f(i, x):
    return i * x / n
 
# u enthält die Funktionswerte zu allen Zeiten i und Orten x.
# Initialisierung.
u = np.zeros((iterationen + 1, n))
# Berechnung der Werte.
for i in range(1, iterationen + 1):
    for x_werte in range(1, n):
        u[i, x_werte] = f(i, x_werte)
 
fig, ax = plt.subplots()
x_werte = np.linspace(0, n, n)
 
def animate(i):
    ax.cla()
    ax.set(xlim=(0, n), ylim=(-100, 100))
    ax.plot(x_werte, u[geschwindigkeit * i])[0]
 
anim = FuncAnimation(fig, animate, interval=1, frames=iterationen // geschwindigkeit)
# anim = FuncAnimation(fig, animate, frames=iterationen)
 
plt.show()

Schwingende Saite simulieren

Bitte Programm ausklappen

import numpy as np
from matplotlib import pyplot as plt
from matplotlib import colormaps
import matplotlib.animation as animation
from matplotlib.animation import FuncAnimation
 
# Grösse des quadratischen Feldes
n = 40
iterationen = 1000
geschwindigkeit = 20 # je höher, desto schneller
 
delta_t = 0.01
 
# Auslenkungen u und Geschwindigkeiten v auf Null setzen für alle Zeiten und $x$-Werte.
u = np.zeros((iterationen + 1, n))
v = np.zeros((iterationen + 1, n))
 
# Randwerte
for i in range(iterationen):
    # Die schwingende Saite ist am Rand befestigt:
    # Auslenkung am Rand ist zu jedem Zeitupunkt Null.
    u[i, 0] = 0
    u[i, n - 1] = 0
    # Geschwindigkeit am Rand ist zu jedem Zeitpunkt Null.
    v[i, 0] = 0
    v[i, n - 1] = 0
print("Randwerte initialisiert (Werte am Rand des Intervalls zu allen Zeiten)")
 
def f(x):
    return np.sin(3 * np.pi * x)
    # Aufgabe: Statt dieser Sinusfunktion nimm andere Funktionen auf dem Intervall [0, 1].
    # Empfehlung: Die Randwerte (also die Werte bei 0 und 1) sollten Null sein.
    # Die Funktion sollte Werte im Intervall [-1, 1] annehmen.
    # Vorschläge: Sinusfunktion mit anderer Sequenz, stückweise lineare Funktion, Parabel.
 
# Startwerte zur Zeit t=0:
for x_werte in range(n):
    # Auslenkung zur Zeit t=0 an der Stelle x:
    u[0, x_werte] = 100 * f(x_werte / (n - 1))
    # Geschwindigkeit zur Zeit t=0 an der Stelle x:
    v[0, x_werte] = 0
print("Startwerte initialisiert (Positionen und Geschwindigkeiten zur Zeit t=0)")
 
# Start der Simulation
for i in range(1, iterationen + 1):
    if i % 100 == 0:
        print(f"Berechnung der Iteration {i}")
    for x_werte in range(1, n - 1):
        v[i, x_werte] = v[i - 1, x_werte] + 0.05
        u[i, x_werte] = u[i - 1, x_werte] + v[i - 1, x_werte] * delta_t
 
fig, ax = plt.subplots()
x_werte = np.linspace(0, n, n)
 
def animate(i):
    ax.cla()
    ax.set(xlim=(0, n), ylim=(-100, 100))
    ax.plot(x_werte, u[geschwindigkeit * i])[0]
 
anim = FuncAnimation(fig, animate, interval=1, frames=iterationen // geschwindigkeit)
 
plt.show()

https://de.wikipedia.org/wiki/Saitenschwingung

Lernen, wie man eine Fläche zeichnet (surface plot)

Bitte Programm ausklappen

import numpy as np
from matplotlib import pyplot as plt
from matplotlib import colormaps
import matplotlib.animation as animation
from matplotlib.animation import FuncAnimation
 
# Grösse des quadratischen Feldes
n = 40
 
u = np.zeros((n, n))
 
def f(z, s):
    return np.sin(np.pi * z) * np.sin(2 * np.pi * s)
 
for z in range(1, n - 1):
    for s in range(1, n - 1):
        u[z, s] = 100 * f(z / (n-1), s/(n-1))
 
(z, s) = np.meshgrid(np.arange(n), np.arange(n))
fig = plt.figure()
koordinatensystem = fig.add_subplot(projection = '3d')
koordinatensystem.set_zlim(-100, 100)
plot = koordinatensystem.plot_surface(z, s, u, cmap = plt.cm.jet, vmin=-100, vmax = 100)
# fig.colorbar(plot, ax = koordinatensystem, shrink = 0.5, aspect = 10)
fig.colorbar(plot, ax = koordinatensystem)
 
 
plt.show()

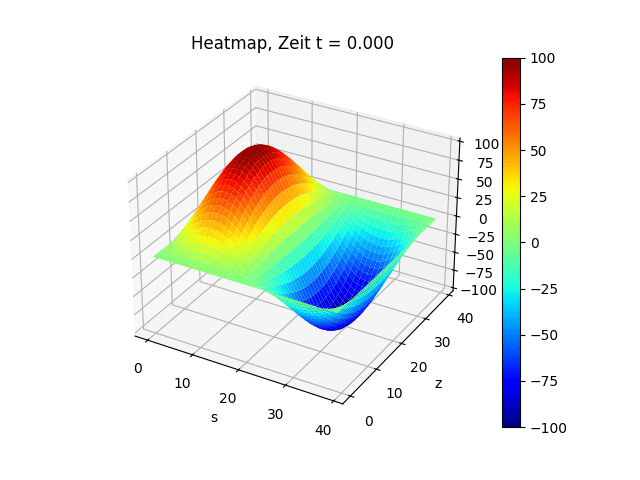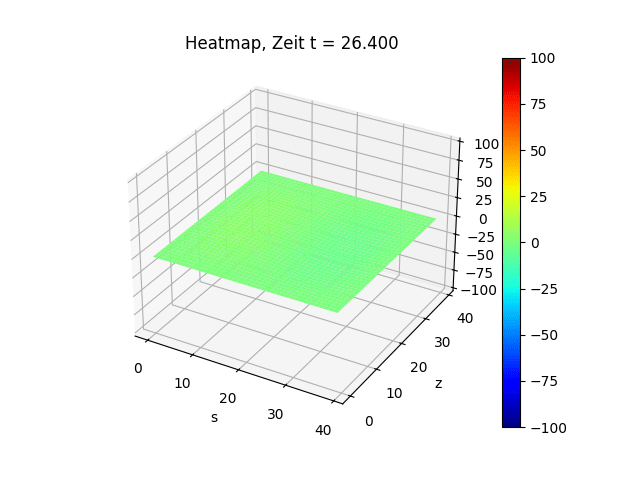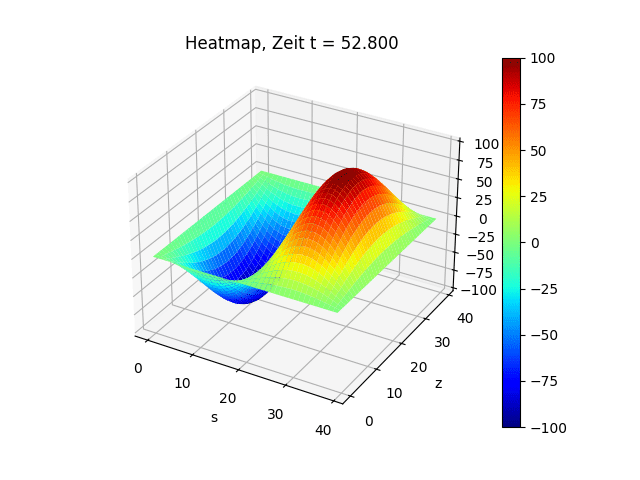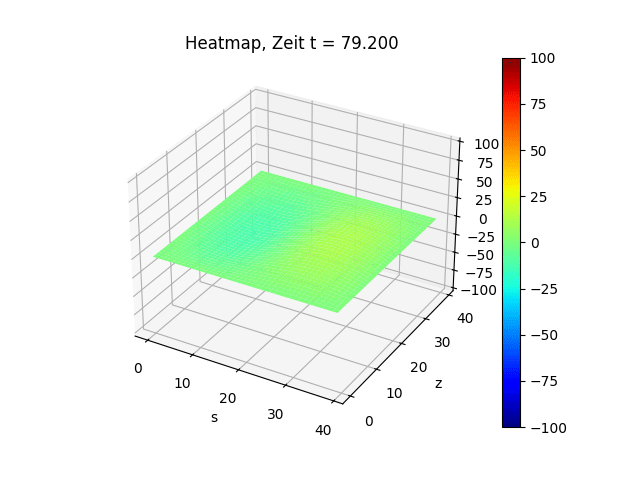
Simulation einer schwingenden Trommel

Bitte Programm ausklappen

import numpy as np
from matplotlib import pyplot as plt
from matplotlib import colormaps
import matplotlib.animation as animation
from matplotlib.animation import FuncAnimation
 
# Grösse des quadratischen Feldes
n = 40
# iterationen = 2600
iterationen = 1000
 
delta_t = 0.02
 
geschwindigkeit = 40
 
u = np.zeros((iterationen + 1, n, n))
v = np.zeros((iterationen + 1, n, n))
 
# Randwerte
for i in range(iterationen):
    for s in range(n):
        u[i, 0, s] = 0
        u[i, n - 1, s] = 0
        v[i, 0, s] = 0
        v[i, n - 1, s] = 0
    for z in range(n):
        u[i, z, 0] = 0
        u[i, z, n - 1] = 0
        v[i, z, 0] = 0
        v[i, z, n - 1] = 0
print("Randwerte initialisiert (Werte am Rand des Quadrats zu allen Zeiten)")
 
def f(z, s):
    return np.sin(np.pi * z) * np.sin(2 * np.pi * s)
 
# Startwerte
for z in range(n):
    for s in range(n):
        u[0, z, s] = 100 * f(z / (n -1), s / (n - 1))
        v[0, z, s] = 0
print("Startwerte initialisiert (Positionen und Geschwindigkeiten zur Zeit t=0)")
 
# Start der Simulation
for i in range(1, iterationen + 1):
    if i % 100 == 0:
        print(f"Simuliert bis zur Zeit {i * delta_t:.1f} bzw. bis Iteration {i}")
    for z in range(1, n - 1):
        for s in range(1, n - 1):
            v[i, z, s] = v[i - 1, z, s] + 0.05
            u[i, z, s] = u[i - 1, z, s] + v[i - 1, z, s] * delta_t
 
 
(z, s) = np.meshgrid(np.arange(n), np.arange(n))
fig = plt.figure()
koordinatensystem = fig.add_subplot(projection = '3d')
koordinatensystem.set_zlim(0, 100)
plot = koordinatensystem.plot_surface(z, s, u[0], cmap = plt.cm.jet, vmin=-100, vmax = 100)
# fig.colorbar(plot, ax = koordinatensystem, shrink = 0.5, aspect = 10)
fig.colorbar(plot, ax = koordinatensystem)
 
def animiere(i):
    j = i * geschwindigkeit
    if i % 10 == 0:
        print(f'Animationsbild zum Iterationsschritt {j}')
    koordinatensystem.cla()
    plt.title(f"Heatmap, Zeit t = {j * delta_t:.3f}")
    plt.xlabel("s")
    plt.ylabel("z")
    koordinatensystem.set_zlim(-100, 100)
    plot = koordinatensystem.plot_surface(z, s, u[i * geschwindigkeit], cmap = plt.cm.jet, vmin=-100, vmax = 100)
    return fig
 
 
anim = animation.FuncAnimation(fig, animiere, interval=1, frames=iterationen // geschwindigkeit, repeat=False)
anim.save("trommel.gif")
 
plt.show()

Simulation

Die beim Simulieren nötige Formel findet sich hier:

# Start der Simulation
for i in range(1, iterationen + 1):
    if i % 100 == 0:
        print(f"Simuliert bis zur Zeit {i * delta_t:.1f} bzw. bis Iteration {i}")
    for z in range(1, n - 1):
        for s in range(1, n - 1):
            v[i, z, s] = v[i - 1, z, s] + ((u[i - 1, z - 1, s] - 2 * u[i - 1, z, s] + u[i - 1, z + 1, s]) + (u[i - 1, z, s - 1] - 2 * u[i - 1, z, s] + u[i - 1, z, s + 1])) * delta_t
            u[i, z, s] = u[i - 1, z, s] + v[i - 1, z, s] * delta_t